TEMA 10
Tema 10: Estimación y/o significación estadística.
La significación estadística (p) esta relacionado con el resultado del estudio. Así, cuando damos un resultado con una p < 0.05 indicamos que la probabilidad de que la relación observada se deba al azar es de 0.05 por 1, y estamos afirmando que el resultado del estudio se cumple, al menos, en el 95% de los casos.
El valor de p no es una medida de fuerza de asociación. Este valor informa sobre la existencia de una diferencia entre ambos grupo y de la probabilidad de que no se deba al azar, pero no informar sobre la causa de las diferencias.
Recordemos que dentro de la estadística inferencial:
- Una de las dos formas de inferencia estadística es el contrates de hipótesis (la otra es la estimación puntual y/o por intervalos).
- Permite contrastar hipótesis y relacionarlo con el método científico.
- Se parte de la hipótesis nula, frente a la hipótesis alternativa.
- Permite calcular el nivel de significación.
- Nos permite tomar decisiones, cuantificando el error.
¿Qué es el constrate de hipótesis?
La prueba o el contraste de hipótesis consiste en contrastar la hipótesis del estudio con los datos obtenidos en la muestra con el fin de verificar si existen diferencias en los hallazgos obtenidos en ambos grupos debidas a la acción de la variableindependiente, o si simplemente estas diferencias han sido fruto del azar.
El contraste de hipótesis nos permite decidir si los resultados obtenidos son fruto de la causalidad (por una relación causa-efecto) o de la casualidad (por azar).
Para poder realizar esta prueba tenemos que seguir una serie de fases:
- FASE 1: se expresa el interrogante de la investigación como una hipótesis estadística.
Normalmente se expresa de la siguiente forma, H0: μA = μB
Es la hipótesis de investigación o alternativa (H1 o Ha) la que afirma que la media de la población es un valor diferente al hipotético.
Se suele expresar de la siguiente forma, H1: μA ≠ μB
Existen dos tipo de hipótesis:
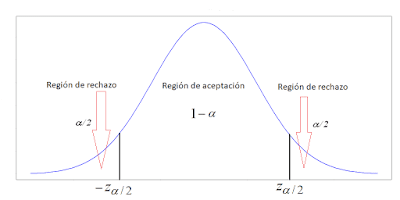
- Las hipótesis no direccionales o bilaterales solo indican que el parámetro de la población es diferente al hipotéticamente establecido, sin especificar si es un valor mayor o menor, y requieren pruebas de hipótesis bilaterales. El valor de α se distribuye en las dos colas de la curva, por lo que cada cola adopta un valor de α /2.
- La hipótesis sea direccional o unilateral, además de afirmar que el parámetro es diferente, indicamos si es mayor o menor. Requeriría un contraste de hipótesis unilateral, teniendo en cuenta solo una cola de la distribución, en la que el valor de α será́ de 0.05. Sin embargo, como ya se ha indicado, la mayoría de las aplicaciones estadísticas realizan un contraste bilateral, para descartar que el efecto que se produce no es el contrario.
- FASE 2: decidir sobre la prueba estadística adecuada.
Tipo de variables que se contrastan
|
Prueba paramétrica
|
Cualitativa + Cualitativa
|
Chi cuadrado
|
Cualitativa de 2 categorías + Cuantitativa
|
T de Student
|
Cualitativa de más de 2 categorías + Cuantitativa
|
ANOVA
|
Cuantitativa + Cuantitativa
|
Correlación de Person
|
- FASE 3: seleccionar grado de significación para la prueba estadística.
Basándose en esta probabilidad, se decidirá́ rechazar o no la hipótesis nula. Así, cuanto
menor sea el valor de p, menor será́ la probabilidad de que los resultados obtenidos se
deban al azar y mayor evidencia habrá́ en contra de la hipótesis nula.
Para decidir si se rechaza o no la H0 debe fijarse previamente un valor de p por debajo
del cual se considera que se dispone de la suficiente evidencia contra la H0 para
rechazarla. Este valor se denomina valor de significación estadística α, que de forma
arbitraria, y por convenio, se fija habitualmente en el 5% (0.05).
Errores de hipótesis.
Con una misma muestra podemos aceptar o rechazar la hipótesis nula, todo dependen
de un error, al que llamamos α. El error α es la probabilidad de equivocarnos al
rechazar la hipótesis nula.



Comentarios
Publicar un comentario